Um sistema de forças, com várias forças.

• Vamos supor uma situação em que três ou mais forças estejam atuando sobre um mesmo corpo, em direções e sentidos diversos. Como iremos determinar a força resultante? Talvez a primeira ideia seja, calcular a resultante entre duas delas e assim sucessivamente até chegar à uma única força, capaz de produzir o mesmo efeito do sistema.

Deve ter observado que é bem complexa a determinação da direção da resultante e, se seguirmos por esse caminho, seremos obrigados a usar as razões trigonométricas seno e cosseno de ângulos aproximados, tornando mais difícil o cálculo. Não é impossível seguir esse caminho, mas é, sem dúvida, o mais complexo. Será tanto mais complexo, quanto maior for o número de forças componentes.

Foi para isso que vimos no estudo da adição de vetores a decomposição em componentes ortogonais. Se aplicarmos esse recurso às forças de nosso sistema, conseguiremos reduzir todas elas a um par de forças ortogonais, e então, aplicando o Teorema de Pitágoras teremos a força resultante, bem mais simples que o processo descrito acima.

Vamos ver como fica a questão? Observe a figura abaixo, onde temos um sistema composto de quatro forças concorrentes.

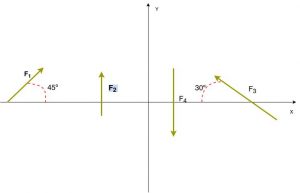
• $\color{Blue}{\vec{F_{1}} = {8\sqrt 2}N } $
• $\color{Brown}{\vec{F_{2}}  = 6 N}$
• $\color{Blue}{\vec{F_{3}} = {10\sqrt{3}} N}$
• $\color{Brown}{\vec{F_{4}} = 8 N}$

Vamos armar o diagrama de forças, transportando todas as componentes para a origem do sistema de eixos $\color{Brown}{\widehat{XOY}}$ e decompor as forças oblíquas em suas componentes ortogonais.

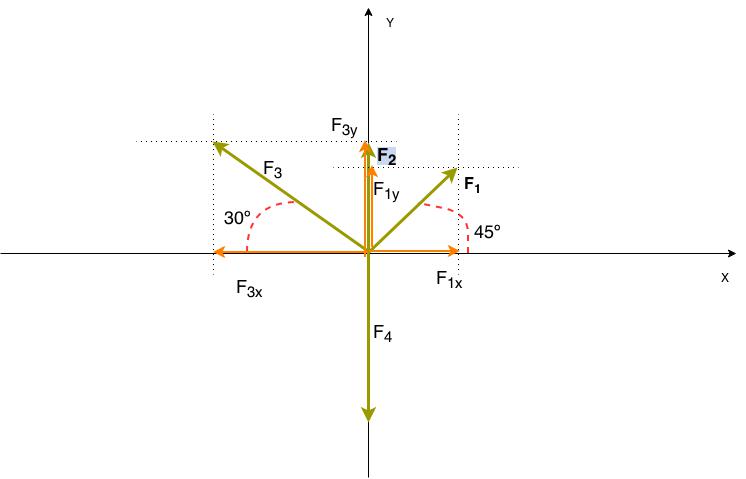
As forças $\color{Blue}{F_{1}}$ e $\color{Blue}{F_{3}}$ são oblíquas em relação aos eixos e vamos fazer sua decomposição nas componentes ortogonais

• $\color{Blue}{\vec{F_{1x}},\vec{F_{1y}},\vec{F_{3x}} e \vec{F_{3y}}} $
• $\color{Green}{\vec{F_{1x}} = \vec{F_{1}}\cdot {cos 45^{0}}  = {8\cdot\sqrt {2}}\cdot {\sqrt {2}}\over{2}}  = {8\sqrt {2}^{2}}\over {2}} = {8\cdot 2\over 2}  = 8,0\,N}$
• $\color{Blue}{\vec{F_{1y}} =\vec{F_{1}}\cdot{sen 45^{0}} = {8,0\cdot\sqrt {2}}\cdot {\sqrt {2}\over 2} = {8,0\sqrt {2}^{2}\over 2} = {8,0\cdot 2\over 2} = 8,0\,N }$
• $\color{Green}{\vec{F_{3x}} = \vec{F_{3}}\cdot{cos 30^{0}}  = {10\cdot\sqrt {3}}\cdot{\sqrt{3}\over 2} = {10\cdot\sqrt {3}^{2}}\over 2}  = {10\cdot 3\over2} = 30\over 3} = 15,0\,N}$
• $\color{Blue}{\vec{F_{3y}} = \overline{F_{3}}\cdot{sen 30^{0}} = {10\cdot 3}\cdot{1\over 2}  = {{10\cdot\sqrt {3}\over 2} = {5\cdot\sqrt {3} N}$

As forças $\color{Blue}{\overline{F_{2}}}$ e $\color{Blue}{\vec{F_{4}}}$, conincidem com a direção do eixo $\color{Brown}{\overline{OY}}$ e portanto suas componentes na direção $\color{Brown}{\overline{OX}}$ são nulas. Resultou agora um sistema com componentes em $\color{Brown}{\overline{OX}}$ e componentes em $\color{Brown}{\overline{OY}}$. Podemos então determinar a resultante em cada uma dessas direções, o que nos fornece as componentes ortogonais do sistema.

• $\color{Blue}{\vec{F_{x}} = \vec{F_{1x}} – \overline{F_{3x}} = {8,0 – 15,0} = -7}$
• $\color{Brown}{\vec{F_{x}}  = – 7,0\,N }$
• $\color{Blue}{\vec{F_{y}} = {F_{1y}} + {F_{2}} + {F_{3y}} – {F_{4}}  = {8,0 + 6,0 + 5\sqrt{3} – 8,0} = {6,0 + 5\cdot{1,73}}= {6,0 + 8,65}}$
• $\color{Brown}{\vec{F_{y}} = 14,65\,N }$

O sistema de forças ortogonais terá a seguinte configuração gráfica.

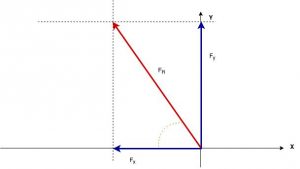
Agora aplicamos o Teorema de Pitágoras na determinação do módulo da força resultante do sistema.

• $\color{Blue}{\vec{F_{R}}^2 = \vec{F_{x}}^2 + \vec{F_{y}}^2 }$
• $\vec{F_{R}}^2 = {- 7,0}^2 + {14,65}^2$
• $\vec{F_{R}}^2 = {49,00 + 214,65 } = 263,65$
• $\color{Brown}{\vec{F_{R}} = \sqrt{263,65} = 16,24 N }$

Vamos determinar a direção da resultante.

• $\color{Blue}{tg\beta ={\vec{F_{y}}\over\vec{F_{x}}}  = {{14,65}\over {-7,0}} = -2,093 }$

Então: $\color{Brown}{\beta = arctg (-2,093)}$

A força resultante tem a direção tal que sua tangente é igual a -2,093, no segundo quadrante, percorrendo o plano cartesiano no sentido anti-horário.

Fica evidente que o número de forças componentes não importa, pois sempre irá resultar um conjunto de forças ortogonais, do qual será obtido um sistema de duas forças ortogonais. Aí reside a grande simplificação desse método de resolução de sistemas com mais de duas forças no plano. 

Para treinar um pouco, deixo alguns exemplos.

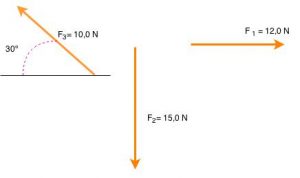
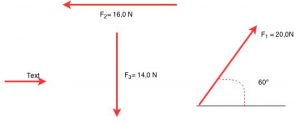
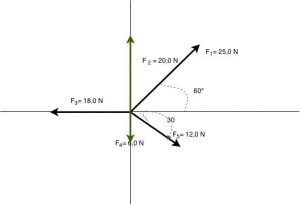
Em caso de dúvida, use qualquer um dos canais abaixo citados para entrar em contato. Estou à sua disposição para sanar as dúvidas.

Obs.: Esse mesmo procedimento será aplicado, quando você, em estudos futuros for determinar resultantes em um sistema tri-dimensional, acrescentando um terceiro eixo. Com pequenas ampliações dos procedimentos, terá a resposta desejada. 

Curitiba, 21 de outubro de 2017 (republicação).

Décio Adams

[email protected]

[email protected]

[email protected]

www.facebook.com/livros.decioadams

www.facebook.com/decio.adams

www.facebook.com/decioadams.matfisonline

@DcioAdams

Telefone: (41) 3019-4760

Celular WhatsApp: (41) 99805-0732

Tags: #decomposição em componentes, #estática, #física, #força resultante, #forças múltiplas, #mecânica, #sistema ortogonal.