FI.ME.006-01 – Física – Mecânica, estática. Grandezas vetoriais e escalares.

By decioadams in Estática, Física, Mecânica 19 de outubro de 2017

Mecânica – Grandezas escalares e vetoriais.

Em toda física, teremos as grandezas com uma outra classificação. Esta feita em função dos requisitos necessários para a perfeita definição das mesmas. Vamos analisar alguns exemplos.

Colocamos um corpo sobre a balança e determinamos a sua massa. O resultado deu $6,0\, kg$. Temos o número que exprime a quantidade de vezes que a massa desse corpo contém a massa de $1,0\, kg$ e logicamente a unidade. Precisamos saber mais alguma coisa a respeito da massa desse corpo para ficar perfeitamente determinada?

A resposta certamente será não.

Marcamos no relógio o tempo transcorrido durante uma viagem entre dois lugares. Vimos que ela foi realizada em $15\, min.$ É necessária mais alguma informação sobre a duração da viagem? É claro que não. Novamente temos apenas o número e a unidade. Qualquer outra informação será somente para ilustrar o evento, mas não acrescenta nenhuma informação importante na determinação da grandeza.

Podemos enumerar uma infinidade de grandezas que ficam perfeitamente conhecidas com um número e uma unidade. A essa informação, número e unidade, denominamos módulo.

As grandezas que ficam perfeitamente determinadas com o módulo, denominamos Grandezas escalares.

Apenas para citar mais alguns casos, vamos ver: a altura de uma pessoa, o comprimento de uma caixa, a temperatura de um corpo, a carga de um corpo eletrizado, etc.

E se recebemos a informação de que determinado bloco de madeira, apoiado sobre uma mesa, recebe a ação de uma força de 5,0 N, temos condições de descrever o comportamento desse corpo sob a ação dessa força?

Parece que logo vamos querer saber como, onde, em que direção e sentido a força é aplicada. Só então poderemos descrever o comportamento do corpo. São possíveis várias situações:

a) A força pode ser aplicada na vertical sobre o meio do corpo, comprimindo o mesmo contra a mesa. Não irá ocorrer nada, não é verdade?
b) A força pode ser aplicada numa extremidade do corpo, agindo na direção horizontal. Pode ser para direita, esquerda ou outra direção. Dependendo do atrito pode ser que o corpo comece a se mover na direção e sentido em que a força atua.
c) A força pode ser aplicada na direção oblíqua, acima ou abaixo da horizontal, puxando ou empurrando o corpo. O comportamento será outro.

Note que a Força precisa de alguma informação a mais para ficar perfeitamente determinada, pois além do módulo, vimos que é importante conhecer o ponto em que ela é aplicada, a direção (vertical, horizontal, inclinada), e o sentido de sua ação. Isso é característica de um grande número de grandezas, especialmente na mecânica.

Estamos diante de grandezas vetoriais. Elas necessitam para podermos avaliar seus efeitos, de módulo, direção, sentido e ponto de aplicação.

Essas características nos levam à necessidade de usarmos, no estudo de problemas envolvendo essas grandezas, alguns recursos além da mera aritmética. Vamos precisar da geometria e especialmente da trigonometria.

Para iniciar, vamos usar um ente geométrico denominado vetor, na representação dessas grandezas.

Vetor é um segmento de reta orientado (Tem uma seta numa ponta).

As extremidades do segmento serão a origem onde o vetor começa e a extremidade onde fica a seta, que indica o sentido da grandeza representada.

Esse segmento de reta nos fornece uma direção que é igual à da reta suporte. Um comprimento que podemos associar ao módulo da grandeza. Um sentido dado pela seta de orientação e um ponto de aplicação, lugar onde o vetor é aplicado. Veja os exemplos abaixo.

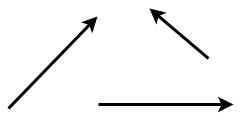
Vetores diversos (1) — Vetores diversos.

Classificação dos vetores:

Colineares se eles forem segmentos da mesma reta.

Vetores colineares (1) — Vetores colineares.

Paralelos se forem segmentos de retas paralelas.

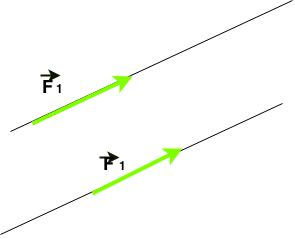
Vetores paralelos (1) — Vetores paralelos.

Coplanares, se as retas de que fazem parte, estiverem no mesmo plano.

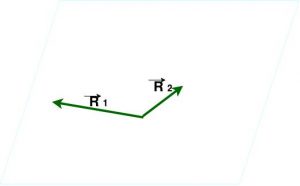
Concorrentes, se as retas tiverem um ponto em comum.

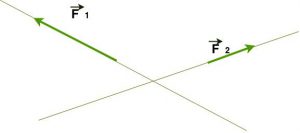
Congruentes, se tiverem o mesmo módulo (comprimento).

Equipolentes, se possuirem o mesmo módulo, a mesma direção e o mesmo sentido.
Ortogonais ou perpendiculares, se formarem entre eles um ângulo reto (90º).

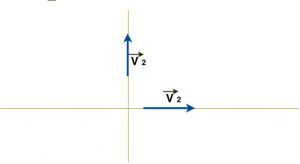
Vetores opostos, tem a mesma direção e sentidos opostos.

Vetores diretamente opostos, tem mesma direção, mesmo módulo e sentidos opostos.

Vetores diretamente opostos — Vetores diretamene opostos.

Associamos a cada vetor (grandeza vetorial) uma letra, geralmente minúscula, encimada por uma pequena seta da esquerda para direita. Vejamos alguns exemplos.